How To Find Acceleration From Average Velocity

Learning Objectives

By the cease of this section, y'all will be able to:

• Calculate the average acceleration between ii points in time.
• Calculate the instantaneous dispatch given the functional form of velocity.
• Explicate the vector nature of instantaneous acceleration and velocity.
• Explicate the difference between boilerplate acceleration and instantaneous dispatch.
• Find instantaneous acceleration at a specified fourth dimension on a graph of velocity versus time.

The importance of understanding dispatch spans our mean solar day-to-day experience, every bit well as the vast reaches of outer infinite and the tiny world of subatomic physics. In everyday chat, to advance means to speed upwards; applying the brake pedal causes a vehicle to deadening downward. Nosotros are familiar with the acceleration of our car, for example. The greater the acceleration, the greater the change in velocity over a given time. Acceleration is widely seen in experimental physics. In linear particle accelerator experiments, for example, subatomic particles are accelerated to very loftier velocities in collision experiments, which tell united states of america information about the structure of the subatomic world as well as the origin of the universe. In infinite, cosmic rays are subatomic particles that have been accelerated to very high energies in supernovas (exploding massive stars) and active galactic nuclei. It is of import to understand the processes that accelerate catholic rays because these rays contain highly penetrating radiation that tin damage electronics flown on spacecraft, for example.

Average Acceleration

The formal definition of acceleration is consistent with these notions just described, but is more inclusive.

Average Acceleration

Boilerplate dispatch is the rate at which velocity changes:

[latex] \overset{\text{–}}{a}=\frac{\text{Δ}5}{\text{Δ}t}=\frac{{v}_{\text{f}}-{v}_{0}}{{t}_{\text{f}}-{t}_{0}}, [/latex]

where [latex] \overset{\text{−}}{a} [/latex] is average acceleration, v is velocity, and t is time. (The bar over the a means average acceleration.)

Because acceleration is velocity in meters divided by time in seconds, the SI units for acceleration are frequently abbreviated one thousand/sⁱⁱ—that is, meters per second squared or meters per second per second. This literally ways by how many meters per second the velocity changes every 2nd. Call up that velocity is a vector—it has both magnitude and direction—which means that a change in velocity can be a alter in magnitude (or speed), but it tin can as well be a change in direction. For example, if a runner traveling at x km/h e slows to a end, reverses management, continues her run at ten km/h due west, her velocity has changed as a issue of the alter in direction, although the magnitude of the velocity is the same in both directions. Thus, dispatch occurs when velocity changes in magnitude (an increase or subtract in speed) or in direction, or both.

Acceleration every bit a Vector

Acceleration is a vector in the same direction equally the change in velocity, [latex] \text{Δ}v [/latex]. Since velocity is a vector, it tin can change in magnitude or in direction, or both. Acceleration is, therefore, a change in speed or direction, or both.

Keep in mind that although acceleration is in the management of the alter in velocity, it is not ever in the direction of motility. When an object slows downward, its acceleration is opposite to the management of its motion. Although this is usually referred to as deceleration (Figure), we say the train is accelerating in a direction opposite to its management of move.

Figure 3.ten A subway train in Sao Paulo, Brazil, decelerates every bit it comes into a station. Information technology is accelerating in a direction opposite to its direction of motion. (credit: Yusuke Kawasaki)

The term deceleration tin crusade confusion in our analysis because information technology is non a vector and it does not point to a specific direction with respect to a coordinate system, so we do not apply it. Dispatch is a vector, so nosotros must choose the advisable sign for information technology in our chosen coordinate system. In the case of the train in (Figure), acceleration is in the negative management in the called coordinate system, so we say the train is undergoing negative dispatch.

If an object in move has a velocity in the positive direction with respect to a called origin and information technology acquires a constant negative acceleration, the object somewhen comes to a rest and reverses direction. If we expect long enough, the object passes through the origin going in the opposite direction. This is illustrated in (Figure).

Effigy iii.11 An object in motion with a velocity vector toward the east nether negative acceleration comes to a balance and reverses direction. It passes the origin going in the contrary direction after a long enough fourth dimension.

Example

Calculating Boilerplate Acceleration: A Racehorse Leaves the Gate

A racehorse coming out of the gate accelerates from rest to a velocity of 15.0 m/due south due westward in one.lxxx south. What is its boilerplate acceleration?

Figure 3.12 Racehorses accelerating out of the gate. (credit: Jon Sullivan)

Strategy

Start we depict a sketch and assign a coordinate system to the problem (Figure). This is a simple problem, just it always helps to visualize it. Find that we assign east as positive and west as negative. Thus, in this instance, we have negative velocity.

Figure 3.13 Place the coordinate system, the given information, and what you want to determine.

Nosotros can solve this trouble by identifying [latex] \text{Δ}5\,\text{and}\,\text{Δ}t [/latex] from the given information, and then calculating the boilerplate acceleration directly from the equation [latex] \overset{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{{v}_{\text{f}}-{v}_{0}}{{t}_{\text{f}}-{t}_{0}} [/latex].

Solution

First, identify the knowns: [latex] {v}_{0}=0,{5}_{\text{f}}=-15.0\,\text{m/s} [/latex] (the negative sign indicates direction toward the west), Δt = i.80 s.

Second, find the modify in velocity. Since the horse is going from zero to –xv.0 chiliad/s, its modify in velocity equals its final velocity:

[latex] \text{Δ}v={five}_{\text{f}}-{v}_{0}={v}_{\text{f}}=-15.0\,\text{k/s}. [/latex]

Final, substitute the known values ([latex] \text{Δ}5\,\text{and}\,\text{Δ}t [/latex]) and solve for the unknown [latex] \overset{\text{–}}{a} [/latex]:

[latex] \overset{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{-15.0\,\text{m/due south}}{1.80\,\text{southward}}=-8.33{\text{m/s}}^{two}. [/latex]

Significance

The negative sign for acceleration indicates that acceleration is toward the due west. An acceleration of 8.33 m/southward^two due w means the horse increases its velocity by 8.33 one thousand/s due west each second; that is, 8.33 meters per second per 2d, which we write as 8.33 thousand/south². This is truly an average acceleration, considering the ride is not smooth. We see later that an dispatch of this magnitude would require the rider to hang on with a forcefulness nearly equal to his weight.

Cheque Your Agreement

Protons in a linear accelerator are accelerated from residual to [latex] ii.0\,×\,{10}^{7}\,\text{thousand/s} [/latex] in ten^–four due south. What is the average dispatch of the protons?

Instantaneous Dispatch

Instantaneous acceleration a, or acceleration at a specific instant in time, is obtained using the same process discussed for instantaneous velocity. That is, we calculate the average velocity between 2 points in time separated by [latex] \text{Δ}t [/latex] and let [latex] \text{Δ}t [/latex] arroyo zero. The result is the derivative of the velocity role v(t), which is instantaneous acceleration and is expressed mathematically every bit

[latex] a(t)=\frac{d}{dt}v(t). [/latex]

Thus, like to velocity being the derivative of the position function, instantaneous acceleration is the derivative of the velocity function. We can testify this graphically in the same style as instantaneous velocity. In (Effigy), instantaneous acceleration at time t ₀ is the slope of the tangent line to the velocity-versus-time graph at time t ₀. Nosotros see that boilerplate dispatch [latex] \overset{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t} [/latex] approaches instantaneous acceleration as [latex] \text{Δ}t [/latex] approaches cipher. Also in part (a) of the figure, we see that velocity has a maximum when its slope is nil. This time corresponds to the zero of the acceleration office. In part (b), instantaneous acceleration at the minimum velocity is shown, which is also aught, since the gradient of the bend is zero there, also. Thus, for a given velocity function, the zeros of the dispatch function requite either the minimum or the maximum velocity.

Figure 3.14 In a graph of velocity versus time, instantaneous acceleration is the gradient of the tangent line. (a) Shown is boilerplate dispatch [latex] \overset{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{{five}_{\text{f}}-{v}_{i}}{{t}_{\text{f}}-{t}_{i}} [/latex] betwixt times [latex] \text{Δ}t={t}_{6}-{t}_{1},\text{Δ}t={t}_{5}-{t}_{two} [/latex], and [latex] \text{Δ}t={t}_{4}-{t}_{3} [/latex]. When [latex] \text{Δ}t\to 0 [/latex], the boilerplate acceleration approaches instantaneous dispatch at time t0. In view (a), instantaneous acceleration is shown for the point on the velocity curve at maximum velocity. At this point, instantaneous acceleration is the slope of the tangent line, which is nix. At any other time, the slope of the tangent line—and thus instantaneous acceleration—would not be zero. (b) Same as (a) but shown for instantaneous acceleration at minimum velocity.

To illustrate this concept, permit's look at two examples. Beginning, a uncomplicated instance is shown using (Effigy)(b), the velocity-versus-time graph of (Figure), to discover acceleration graphically. This graph is depicted in (Figure)(a), which is a direct line. The corresponding graph of acceleration versus time is found from the gradient of velocity and is shown in (Effigy)(b). In this example, the velocity function is a straight line with a constant slope, thus acceleration is a constant. In the side by side example, the velocity function has a more complicated functional dependence on time.

Effigy 3.fifteen (a, b) The velocity-versus-fourth dimension graph is linear and has a negative abiding slope (a) that is equal to dispatch, shown in (b).

If we know the functional form of velocity, v(t), we tin can calculate instantaneous acceleration a(t) at any fourth dimension bespeak in the motion using (Figure).

Example

Calculating Instantaneous Acceleration

A particle is in movement and is accelerating. The functional form of the velocity is [latex] five(t)=20t-five{t}^{two}\,\text{m/s} [/latex].

1. Find the functional form of the acceleration.
2. Find the instantaneous velocity at t = one, 2, three, and 5 s.
3. Discover the instantaneous acceleration at t = ane, 2, 3, and 5 s.
4. Interpret the results of (c) in terms of the directions of the dispatch and velocity vectors.

Strategy

We find the functional form of acceleration by taking the derivative of the velocity office. Then, we summate the values of instantaneous velocity and acceleration from the given functions for each. For part (d), we demand to compare the directions of velocity and acceleration at each fourth dimension.

Solution

1. [latex] a(t)=\frac{dv(t)}{dt}=20-10t\,{\text{m/s}}^{2} [/latex]
2. [latex] v(ane\,\text{s})=fifteen\,\text{m/southward} [/latex], [latex] v(ii\,\text{s})=20\,\text{m/southward} [/latex], [latex] five(three\,\text{s})=fifteen\,\text{thou/s} [/latex], [latex] v(5\,\text{s})=-25\,\text{grand/southward} [/latex]
3. [latex] a(i\,\text{s})=10{\,\text{m/due south}}^{2} [/latex], [latex] a(2\,\text{south})=0{\,\text{m/s}}^{2} [/latex], [latex] a(3\,\text{southward})=-x{\,\text{one thousand/s}}^{2} [/latex], [latex] a(5\,\text{s})=-30{\,\text{k/s}}^{ii} [/latex]
4. At t = 1 s, velocity [latex] v(ane\,\text{due south)}=15\,\text{m/s} [/latex] is positive and dispatch is positive, so both velocity and acceleration are in the same management. The particle is moving faster.

At t = 2 s, velocity has increased to[latex] v(two\,\text{southward)}=20\,\text{m/s} [/latex], where it is maximum, which corresponds to the fourth dimension when the acceleration is null. We see that the maximum velocity occurs when the slope of the velocity function is zero, which is but the zero of the acceleration function.

At t = iii due south, velocity is [latex] v(3\,\text{s)}=xv\,\text{m/due south} [/latex] and acceleration is negative. The particle has reduced its velocity and the dispatch vector is negative. The particle is slowing downwards.

At t = five southward, velocity is [latex] v(five\,\text{s)}=-25\,\text{m/s} [/latex] and acceleration is increasingly negative. Between the times t = 3 s and t = 5 s the particle has decreased its velocity to zero and then become negative, thus reversing its direction. The particle is now speeding upwards again, simply in the opposite direction.

Nosotros tin can encounter these results graphically in (Figure).

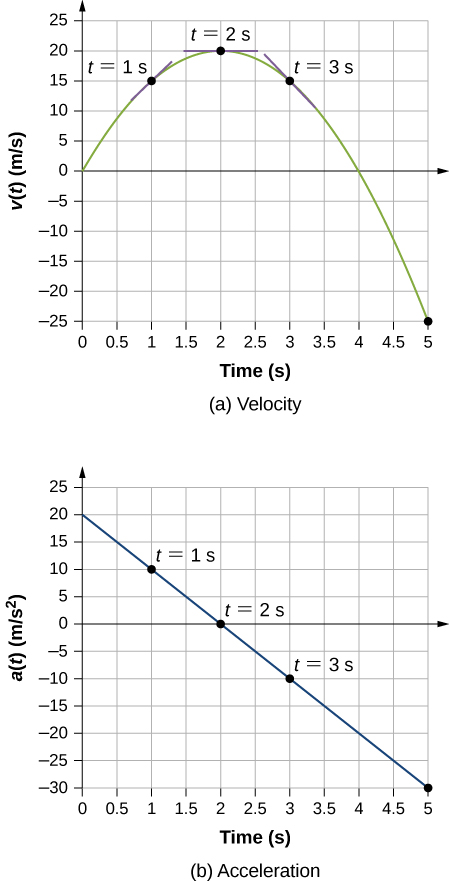
Figure three.sixteen (a) Velocity versus time. Tangent lines are indicated at times 1, 2, and 3 southward. The slopes of the tangent lines are the accelerations. At t = 3 due south, velocity is positive. At t = 5 south, velocity is negative, indicating the particle has reversed management. (b) Acceleration versus time. Comparison the values of accelerations given by the black dots with the respective slopes of the tangent lines (slopes of lines through black dots) in (a), we see they are identical.

Significance

By doing both a numerical and graphical analysis of velocity and dispatch of the particle, we tin learn much about its motion. The numerical analysis complements the graphical assay in giving a total view of the motility. The nada of the acceleration office corresponds to the maximum of the velocity in this example. Likewise in this example, when acceleration is positive and in the same direction as velocity, velocity increases. As acceleration tends toward zero, somewhen condign negative, the velocity reaches a maximum, subsequently which information technology starts decreasing. If we wait long enough, velocity also becomes negative, indicating a reversal of direction. A existent-world case of this type of motion is a car with a velocity that is increasing to a maximum, after which it starts slowing down, comes to a stop, then reverses direction.

Check Your Understanding

An airplane lands on a runway traveling eastward. Describe its acceleration.

Show Solution

If we have east to exist positive, then the airplane has negative acceleration considering information technology is accelerating toward the westward. It is likewise decelerating; its dispatch is reverse in direction to its velocity.

Getting a Feel for Dispatch

You are probably used to experiencing acceleration when you pace into an lift, or step on the gas pedal in your car. However, acceleration is happening to many other objects in our universe with which nosotros don't have straight contact. (Figure) presents the acceleration of various objects. We tin can see the magnitudes of the accelerations extend over many orders of magnitude.

Typical Values of Dispatch(credit: Wikipedia: Orders of Magnitude (dispatch))

Acceleration	Value (thousand/s2)
High-speed railroad train	0.25
Elevator	two
Chetah	5
Object in a free fall without air resistance near the surface of Globe	9.8
Infinite shuttle maximum during launch	29
Parachutist peak during normal opening of parachute	59
F16 aircraft pulling out of a swoop	79
Explosive seat ejection from aircraft	147
Sprint missile	982
Fastest rocket sled peak dispatch	1540
Jumping flea	3200
Baseball struck by a bat	30,000
Closing jaws of a trap-jaw emmet	one,000,000
Proton in the big Hadron collider	[latex] 1.9\,×\,{x}^{ix} [/latex]

In this table, we run across that typical accelerations vary widely with different objects and have nothing to practice with object size or how massive information technology is. Acceleration tin can besides vary widely with time during the movement of an object. A elevate racer has a big dispatch only after its start, but then it tapers off every bit the vehicle reaches a constant velocity. Its average acceleration can be quite different from its instantaneous acceleration at a item time during its move. (Figure) compares graphically boilerplate acceleration with instantaneous dispatch for two very different motions.

Figure 3.17 Graphs of instantaneous acceleration versus fourth dimension for ii unlike ane-dimensional motions. (a) Acceleration varies only slightly and is ever in the same direction, since it is positive. The average over the interval is almost the same every bit the acceleration at whatever given time. (b) Acceleration varies greatly, perhaps representing a package on a postal service office conveyor belt that is accelerated frontward and astern equally it bumps along. It is necessary to consider small-scale time intervals (such equally from 0–1.0 s) with abiding or nearly constant acceleration in such a situation.

Learn about position, velocity, and acceleration graphs. Movement the footling man back and forth with a mouse and plot his move. Set the position, velocity, or acceleration and allow the simulation motion the human for you. Visit this link to use the moving homo simulation.

Summary

• Acceleration is the charge per unit at which velocity changes. Acceleration is a vector; it has both a magnitude and management. The SI unit of measurement for acceleration is meters per 2d squared.
• Acceleration tin can be caused by a alter in the magnitude or the direction of the velocity, or both.
• Instantaneous acceleration a(t) is a continuous part of time and gives the acceleration at any specific fourth dimension during the motion. It is calculated from the derivative of the velocity office. Instantaneous acceleration is the slope of the velocity-versus-time graph.
• Negative acceleration (sometimes chosen deceleration) is dispatch in the negative direction in the chosen coordinate organisation.

Conceptual Questions

Is it possible for speed to be constant while acceleration is non zilch?

Show Solution

No, in one dimension constant speed requires zero acceleration.

Is it possible for velocity to be constant while acceleration is not zero? Explain.

Give an example in which velocity is zero yet acceleration is non.

Show Solution

A ball is thrown into the air and its velocity is nada at the apex of the throw, simply acceleration is not cypher.

If a subway train is moving to the left (has a negative velocity) and then comes to a stop, what is the direction of its acceleration? Is the acceleration positive or negative?

Plus and minus signs are used in one-dimensional movement to indicate direction. What is the sign of an acceleration that reduces the magnitude of a negative velocity? Of a positive velocity?

Prove Solution

Plus, minus

A cheetah can accelerate from residual to a speed of 30.0 m/s in seven.00 s. What is its dispatch?

Show Solution

[latex] a=iv.29{\text{chiliad/s}}^{2} [/latex]

Dr. John Paul Stapp was a U.S. Air Forcefulness officeholder who studied the effects of extreme acceleration on the human body. On Dec x, 1954, Stapp rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015 km/h) in five.00 s and was brought jarringly back to balance in merely 1.40 s. Calculate his (a) acceleration in his direction of movement and (b) acceleration opposite to his direction of motion. Express each in multiples of g (9.fourscore m/south²) by taking its ratio to the dispatch of gravity.

Sketch the acceleration-versus-fourth dimension graph from the following velocity-versus-fourth dimension graph.

Bear witness Answer

A commuter backs her car out of her garage with an acceleration of 1.40 yard/south². (a) How long does it take her to reach a speed of 2.00 thou/southward? (b) If she then brakes to a stop in 0.800 south, what is her dispatch?

Assume an intercontinental ballistic missile goes from rest to a suborbital speed of 6.50 km/s in 60.0 due south (the actual speed and fourth dimension are classified). What is its average acceleration in meters per second and in multiples of k (9.lxxx m/s²)?

Bear witness Solution

[latex] a=eleven.1g [/latex]

An airplane, starting from rest, moves down the track at constant dispatch for 18 due south and then takes off at a speed of threescore m/south. What is the average acceleration of the plane?

Glossary

boilerplate acceleration

the rate of change in velocity; the modify in velocity over time

instantaneous acceleration

acceleration at a specific point in fourth dimension

Source: https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/3-3-average-and-instantaneous-acceleration/

Posted by: truemansweeng.blogspot.com

Share this post